NeurIPS Spotlight | 压缩 LoRA 400倍!Uni-LoRA:仅需一个向量,微调千亿大模型!
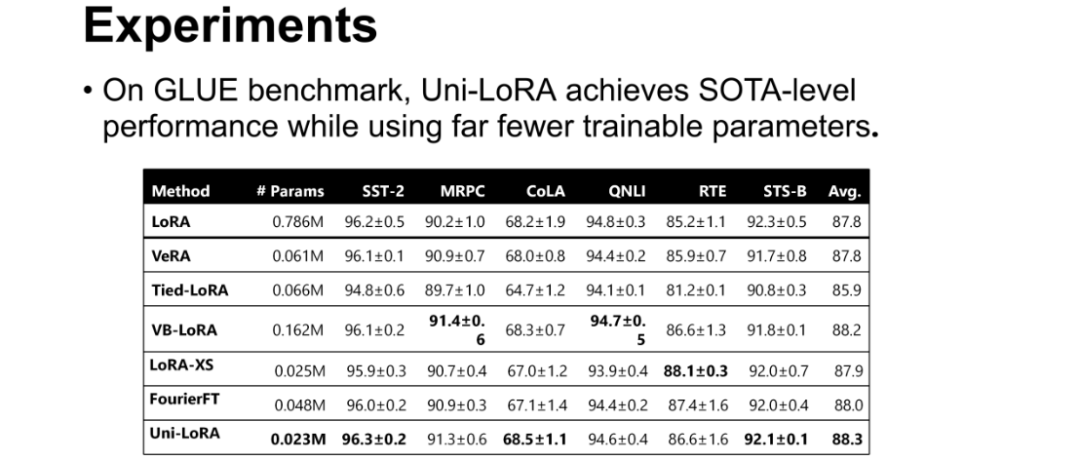
众多研究者致力于在减少可训练参数的同时,保持模型性能稳定。在 MRPC、SST-2、CoLA 等多个子任务中,Uni-LoRA 仅使用0.023M可训练参数,却取得了88.3的平均分数,超越了LoRA(0.786M参数,平均87.8分)、VeRA(0.061M参数,平均87.8分)等主流方法,实现了“以更少参数达更优性能”的目标;这些方法的共性在于,均是将 LoRA 参数投影到结构化的低维子空间中
点击蓝字

关注我们
AI TIME欢迎每一位AI爱好者的加入!
作者简介
李开阳,康涅狄格大学博士生
内容简介
低秩适应(Low-Rank Adaptation,LoRA)通过将权重更新限制在低秩矩阵中,已经成为大型语言模型(LLMs)最常用的参数高效微调(PEFT)方法。近期的一些工作,如 Tied-LoRA、VeRA 和 VB-LoRA,通过加入额外的结构或约束,进一步减少了可训练参数的规模,提高了参数效率。在本文中,我们指出:这些 LoRA 变体所依赖的“参数空间压缩”策略,其实都可以放在一个统一的框架 —— Uni-LoRA 中进行形式化表达。在这一框架下,LoRA 的所有可训练参数都被视为高维向量空间 ℝD 中的元素,而模型实际训练的变量来自一个更小的低维子空间 ℝd(其中 d≪D ),并通过一个投影矩阵 P∈ ℝD×d 重构回原空间。我们发现,不同 LoRA 方法之间最本质的差异,其实就是投影矩阵P 的选择方式。
当前许多 LoRA 变体依赖分层投影或特定结构化的投影矩阵,这虽然实现了参数压缩,但会限制跨层参数共享,从而在一定程度上影响参数效率。基于这一观察,我们提出一种高效且具有理论依据的等距投影矩阵。它支持跨层的全局参数共享,并显著降低计算成本。更重要的是,在 Uni-LoRA 的统一视角下,这一设计使得只需训练 一个向量 就能重构整个大型语言模型的 LoRA 参数 —— 这让 Uni-LoRA 既是一个统一分析框架,也是一种真正意义上的“单向量 LoRA”解决方案。我们在 GLUE、数学推理以及指令微调等基准上进行了大量实验,结果显示:Uni-LoRA 在保持预测性能不下降的同时,实现了目前最高的参数效率,整体表现优于或不逊于现有方法。
论文地址:https://arxiv.org/pdf/2506.00799
代码链接:https://github.com/KaiyangLi1992/Uni-LoRA
论文解读
这项研究聚焦于模型参数轻量化优化,基于LoRA(Low-Rank Adaptation)方法展开创新,核心目标是通过更少的可训练参数,实现与现有模型相当甚至更优的性能表现。“Uni-LoRA”这一命名蕴含双重含义:一方面,“Uni”取自“Uniform”,代表我们提出了一个能够统一过往相关研究的框架;另一方面,“Uni”也源自“Unique”,寓意该方法在参数高效微调领域具备独特的创新性。
在模型压缩与高效AI的研究领域中,LoRA 及其变体已成为参数高效微调(PEFT)的重要技术方向。众多研究者致力于在减少可训练参数的同时,保持模型性能稳定。从 LoRA 到 V-LoRA、VeRA、FourierFT 等方法,可训练参数规模逐步缩减,但模型性能并未出现显著下滑。
基于这一研究现状,我们的核心贡献主要体现在两方面:
1. 提出了一个统一的框架,该框架揭示了所有 LoRA 变体本质上都是 LoRA 空间的低维投影,能够将过往六七种 LoRA 变体的技术逻辑纳入其中,实现了对这类方法的系统性整合;
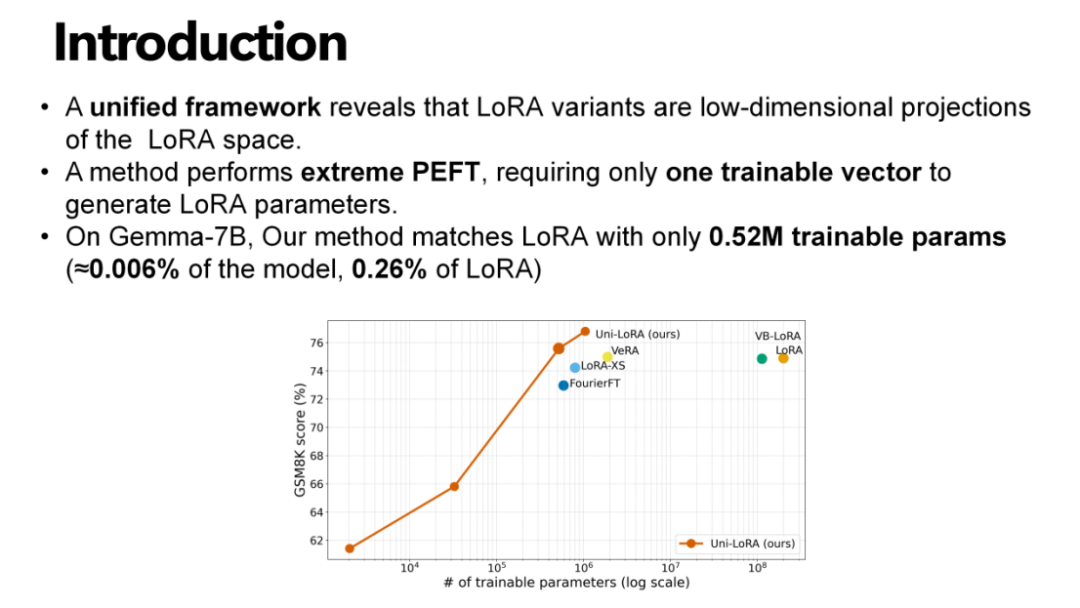
2. 在该统一框架的指导下,提出了一种极致的参数高效微调方法,仅需训练一个向量即可生成 LoRA 参数。以 Gemma-7B 模型为例,我们的方法仅需0.52M可训练参数(约占模型总参数的0.006%,仅为 LoRA 方法参数量的0.26%),却能达到与 LoRA 相当的性能水平。
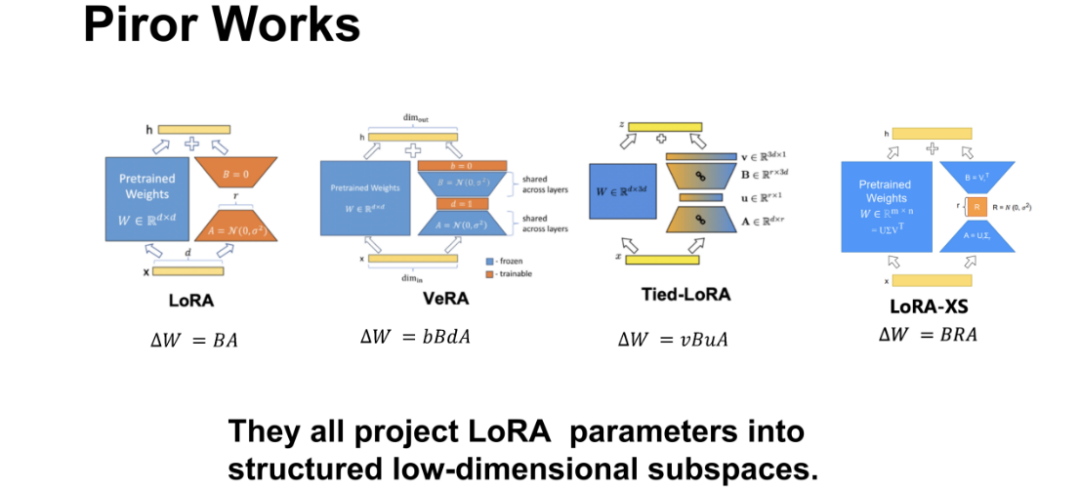
回顾现有研究,LoRA 的核心思路是将模型权重更新量ΔW 分解为两个低秩矩阵B与A的乘积( ΔW=BA ),通过训练这两个低秩矩阵实现参数高效微调。后续变体在此基础上不断优化:
-
VeRA 方法将 ΔW 表示为 bBdA 的形式,固定大矩阵A和B的大部分区域,仅训练对角矩阵d和小矩阵b,大幅减少了可训练参数;
-
Tied-LoRA 通过让不同 LoRA 模块共享矩阵A和B,实现参数复用;
-
LoRA-XS则固定矩阵A和B,仅训练中间一个小尺寸的 R×R 矩阵,进一步压缩参数规模。
这些方法的共性在于,均是将 LoRA 参数投影到结构化的低维子空间中进行训练,本质上都是通过子空间投影实现参数压缩,但各类方法的投影逻辑相对独立,缺乏全局统一的视角。
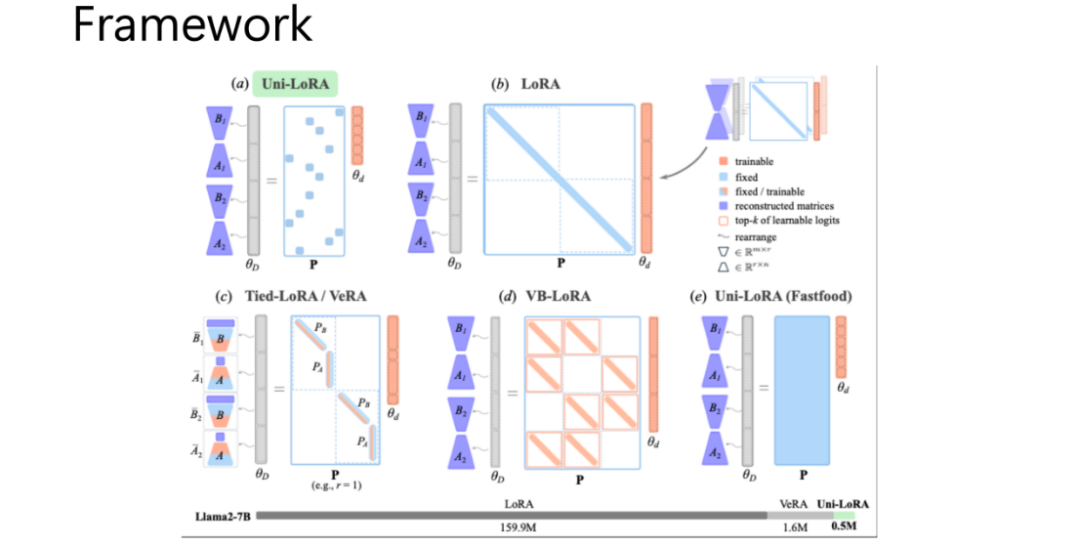
为解决这一问题,我们构建了全局化的统一框架。具体实现逻辑如下:
-
将模型中所有 LoRA 模块的矩阵A和B进行扁平化处理,转化为向量形式;
-
拼接所有 LoRA 模块对应的扁平化向量,形成一个维度极高的向量θD,该向量可视为整个 LoRA 空间的完整表征;
-
假设我们的训练过程在一个低维子空间中进行,该子空间由可训练向量θd(d≪D)表征,通过一个投影矩阵P 将低维子空间的向量θd 投影回高维 LoRA 空间,得到重构矩阵θD=Pθd 。
在这一框架下,不同 LoRA 变体的差异仅在于投影矩阵P 的结构设计。例如,原始 LoRA 方法对应的投影矩阵P是对角方阵,仅对角元素为1,其余为0;VeRA 对应的投影矩阵P 则为稀疏矩阵,通过特定行和列的投影实现参数训练。
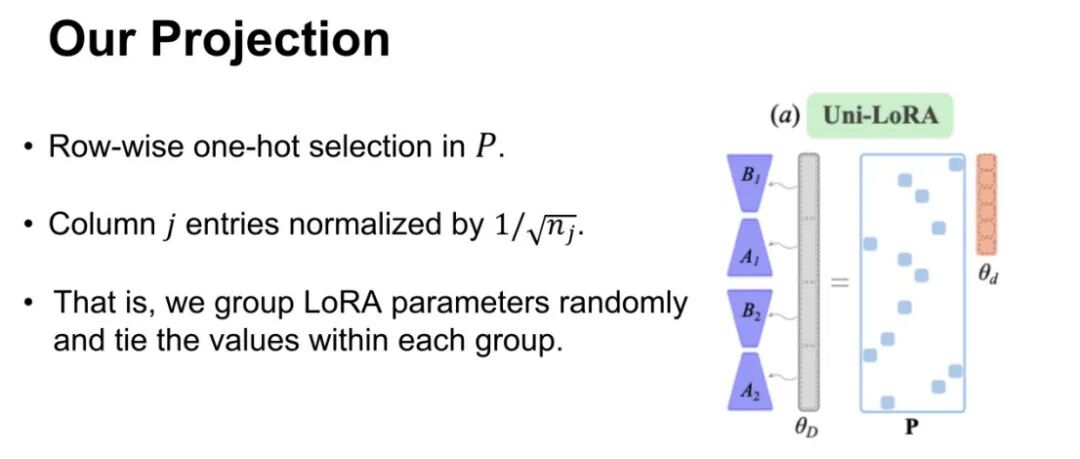
我们设计的投影矩阵P 具有两大核心特性,这也是 Uni-LoRA 实现高效压缩的关键:
-
行向独热选择:在投影矩阵P 的每一行中随机选择一个元素设为非零,其余元素均为0;
-
列归一化处理:对每一列的非零元素按照1/√nj 进行归一化(其中nj 为第j 列的非零元素个数)。
该方法本质上是通过随机分组将 LoRA 参数划分为多个组,强制每组内的参数共享相同值。
核心优势:
-
全局性(Globality):实现跨层参数共享,最大程度减少信息冗余。不同于 VeRA 等局部方法将单个LoRA 模块投影到固定长度的子向量,我们的方法可将任意层的信息随机投影到整个高维空间,适配不同层的信息密度差异;
-
均匀性(Uniformity):将原始高维空间的维度均匀分布到低维子空间,实现均衡的信息映射,确保每个维度的信息传输效率一致;
-
等距性(Isometry):投影过程能够保持参数空间中的距离和几何结构,即对任意两个向量x、y,满足∥P(x−y)∥=∥x−y∥。这一特性使得 LoRA 空间的优化曲面在低维子空间中得以完整保留,原始 LoRA方法中使用的 Adam 等优化算法依然适用。
此外,投影矩阵P 为随机生成,仅需存储随机种子即可,无需额外存储完整矩阵;同时其稀疏特性使得投影过程的时间和空间复杂度均控制在O(D)级别,相比高斯投影、Fastfood等传统等距投影方法,计算效率大幅提升。
我们在多个基准测试和模型上对Uni-LoRA进行了性能验证,实验结果充分证明了方法的有效性:
-
GLUE基准测试:在 MRPC、SST-2、CoLA 等多个子任务中,Uni-LoRA 仅使用0.023M可训练参数,却取得了88.3的平均分数,超越了LoRA(0.786M参数,平均87.8分)、VeRA(0.061M参数,平均87.8分)等主流方法,实现了“以更少参数达更优性能”的目标;
-
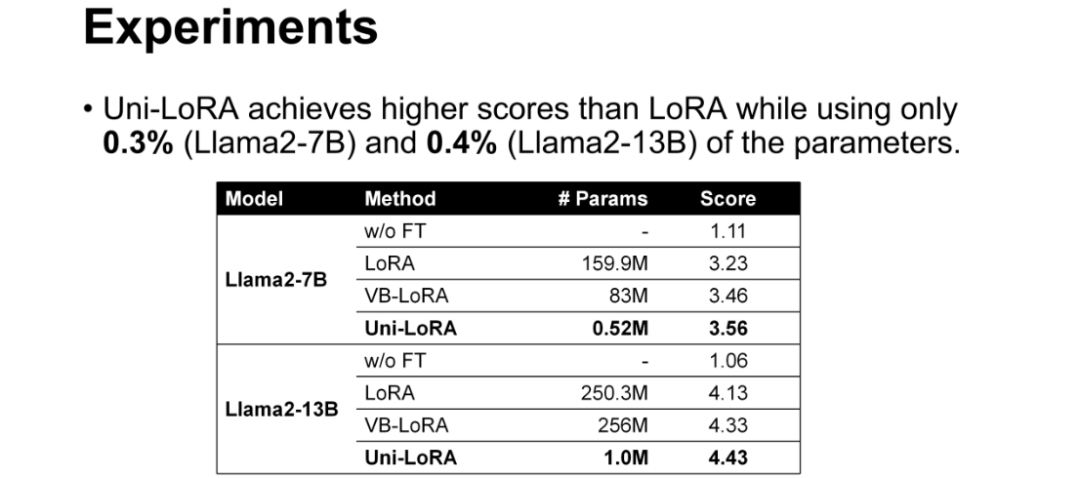
大语言模型测试:在 Llama2-7B 模型上,Uni-LoRA使用0.52M参数(仅为LoRA的0.3%),取得3.56的分数,高于LoRA(3.23分)和VB-LoRA(3.46分);在 Llama2-13B 模型上,1.0M参数(LoRA的0.4%)对应的分数为4.43,同样优于其他对比方法;
-
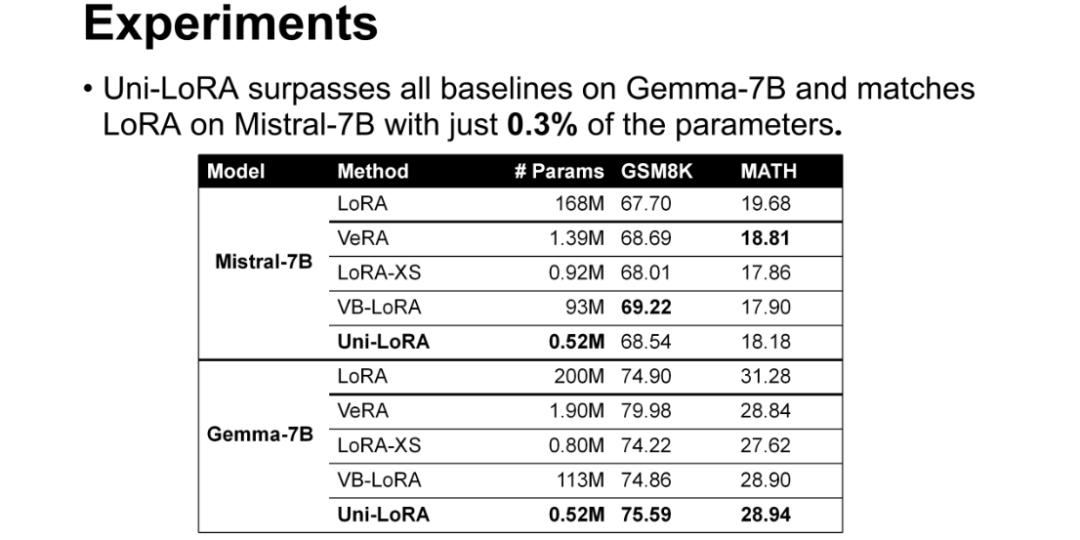
数学推理任务测试:在 Mistral-7B模型上,Uni-LoRA以0.52M参数(LoRA的0.3%)取得68.54的GSM8K分数和18.18的MATH分数,与LoRA(67.70、19.68)性能相当;在 Gemma-7B 模型上,该方法的 GSM8K 分数达到75.59,超过 LoRA 的74.90,MATH 分数28.94与 LoRA 的31.28接近,充分证明了其在复杂推理任务中的有效性。
Uni-LoRA 通过构建统一框架实现了对 LoRA 变体的系统性整合,其创新的投影矩阵设计在保证模型性能的前提下,极大地压缩了可训练参数规模,同时降低了存储成本和传输成本。该方法不仅为参数高效微调提供了新的技术思路,也为大模型的轻量化部署提供了更具可行性的解决方案。
本期文章由支昕整理
往期精彩文章推荐
关于AI TIME
AI TIME源起于2019年,旨在发扬科学思辨精神,邀请各界人士对人工智能理论、算法和场景应用的本质问题进行探索,加强思想碰撞,链接全球AI学者、行业专家和爱好者,希望以辩论的形式,探讨人工智能和人类未来之间的矛盾,探索人工智能领域的未来。
迄今为止,AI TIME已经邀请了2000多位海内外讲者,举办了逾800场活动,超1000万人次观看。

我知道你
在看
提出观点,表达想法,欢迎
留言

点击 阅读原文 查看作者直播回放!
更多推荐
 已为社区贡献1条内容
已为社区贡献1条内容






所有评论(0)